$$
\newcommand{\SetN}{\mathbb{N}}
\newcommand{\SetR}{\mathbb{R}}
\newcommand{\SetC}{\mathbb{C}}
\newcommand{\SetK}{\mathbb{K}}
\newcommand{\SetZ}{\mathbb{Z}}
\newcommand{\SetQ}{\mathbb{Q}}
\newcommand{\SetU}{\mathbb{U}}
\newcommand\ds[0]{\displaystyle}
\newcommand\PCar[1]{\large{\chi}_{#1}}
\newcommand{\=}{\:=\:}
\newcommand\tendvers[2]{\displaystyle\mathop{\longrightarrow}_{#1\rightarrow#2}}
\newcommand\tr[0]{\:^t\!}
\newcommand\limite[2]{\displaystyle\mathop{\text{lim}}_{#1\rightarrow#2}\:}
\newcommand\Sup[1]{\displaystyle\mathop{sup}_{#1}}
\newcommand\Inf[1]{\displaystyle\mathop{inf}_{#1}}
\newcommand\Haut[1]{}
\newcommand\vect[1]{\overrightarrow{#1}}
\newcommand\tendversCU[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CU}}\:}
\newcommand\tendversCS[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CS}}\:}
\newcommand\tendversCN[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CN}}\:}
\newcommand\tendversCUS[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CUS}}\:}
\newcommand\tendversNorme[1]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{#1}\:}
\newcommand\simL[0]{\displaystyle\mathop{\sim}_{^{^L}}}
\newcommand\simC[0]{\displaystyle\mathop{\sim}_{^{^C}}}
\newcommand\simLC[0]{\displaystyle\mathop{\sim}_{^{^{LC}}}}
\newcommand\fonction[5]{
\begin{array}{cccc}
#1\::\:& #2 & \rightarrow & #3 \\
& #4 & \mapsto & \ds #5 \
\end{array}}
$$
| Liste chapitres |
Plan du chapitre |
 | Section |  |
|
 | sous-section |  |
|
|
|
| Ici sera la liste des chapitres !!! |
|
II. Paramètre réel dans l'intégrale.
II.1. Problématique
Que cherche-t-on à faire ?
Soient $D$ et $I$ deux intervalles de $\SetR$ non vides. Dans ce paragraphe, on cherche à pouvoir étudier une fonction définie par une intégrale, c'est-à-dire une application du type :
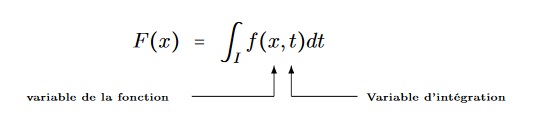
avec $(x,t)\mapsto f(x,t)$ une application de $D\times I$ dans $\SetK$.
|
II. Paramètre réel dans l'intégrale.
II.2. Limite
Théorème de convergence dominée à paramètre continu. 10
Considérons des fonctions $f$ et $F$ comme dans la problématique du début de paragraphe. Notons de plus $a$ dans $\overline{D}$ et $l$ une application de $I$ dans $\SetR$.
$$
\exists g\in\mathcal{C}_m(I,\SetR^+),\:\:\left\{\begin{array} {ll}%
f(x,t)\tendvers{x}{a} l(t)\\
\Haut{0.6}\:t\mapsto f(x,t)\text{ et }t\mapsto l(t)\text{ sont continues par morceaux}&^{(*)}\\[0.15cm]
\Haut{0.6}\:g\:\hbox{ intégrable sur }I&^{(CD)}\\[0.15cm]
\Haut{0.6}\:\forall (x,t)\in D\times I,\:\:|f(x,t)|\leq g(t) &^{(CD)}\\
\end{array}%
\right.
$$
alors $l$ est intégrable et $\ds\int_{_I}\limite{x}{a}f(x,t)\=\limite{x}{a}\int_{_I}f(x,t)$
Remarques.
- Ainsi, pour trouver la limite d'une fonction définie par une intégrale, on utilise le théorème de convergence dominée à paramètre continu.
- C'est exactement le même théorème que le théorème de convergence dominée en remplaçant les $n$ par des $x$.
- Les hypothèses $(CD)$ sont les hypothèses de domination.
- Les hypothèses $(*)$ ne sont utiles qu'à donner un sens aux intégrales.
- La fonction $g$ présente dans les hypothèses de domination est indépendante du paramètre $($ici $x)$ et ne dépend donc que de $t$.
Exercice.11
Considérons la fonction $$F(x)=\int_0^{+\infty}\frac{\sin^2(y)}{x^2+y^2}dy$$
- Déterminer le domaine de définition de $F$.
- Déterminer les limites de $F$ aux bornes de son domaine de définition.
|
II. Paramètre réel dans l'intégrale.
II.3. Continuité et dérivabilité.
Théorème - Continuité.12
Avec les notations de $f$ et $F$ de début de paragraphe, si pour tout segment $[a,b]$ de $D$, il existe $g$ dans $\mathcal{C}_m(I,\SetR^+)$ telle que :
$$\left\{\begin{array} {ll}%
x\mapsto f(x,t)\hbox{ est continue pour tout $t$ de $I$}\\
\Haut{0.6}t\mapsto f(x,t)\hbox{ continue par morceaux pour tout $x$ de }D&^{(*)}\\
\Haut{0.6}\forall x\in [a,b]\subset D,\:\:|f(x,t)|\:\leq\: g(t)&^{(CD)}\\
\Haut{0.6}g\hbox{ intégrable sur }I&^{(CD)}\\
\end{array}%
\right.$$
alors $F$ est continue sur $D$.
Théorème - Dérivabilité.13
Avec les notations de $f$ et $F$ de début de paragraphe, si pour tout segment $[a,b]$ de $D$, il existe $g$ dans $\mathcal{C}_m(I,\SetR^+)$ telle que :
$$\left\{\begin{array} {ll}%
x\mapsto f(x,t)\hbox{ est de classe $C^1$ pour tout $t$ de $I$}\\
\Haut{0.6}t\mapsto f(x,t)\hbox{ continue par morceaux pour tout $x$ de }D&^{(*)}\\
\Haut{0.6}t\mapsto f(x,t)\hbox{ intégrable sur }I&^{(*)}\\
\Haut{0.6}t\mapsto \frac{\delta f}{\delta x}(x,t)\hbox{ continue par morceaux pour tout $x$ de }D&^{(*)}\\
\Haut{0.6}\forall x\in [a,b]\subset D,\:\:\left|\frac{\delta f}{\delta x}(x,t)\right|\:\leq\: g(t)&^{(CD)}\\
\Haut{0.6}g\hbox{ intégrable sur }I&^{(CD)}\\
\end{array}%
\right.$$
alors $F$ est de classe $C^1$ sur $D$ et $F'(x)\=\ds\int_{I}\hbox{$\frac{\delta f}{\delta x}$}(x,t)dt$
Attention !
En pratique, dans les deux théorèmes précédents, on vérifie l'hypothèse de domination sur tout segment $[a,b]$ de $D$ $($ou tout autre intervalle adapté à la situation$)$. En effet montrer qu'une fonction est $C^0$ ou $C^1$ sur intervalle $D$ est équivalent à montrer qu'elle est $C^0$ ou $C^1$ sur tout segment de cet intervalle.
Remarques.
- Les conditions $(*)$ sont les conditions qui permettent de donner un sens aux intégrales présentes dans le théorème. Ainsi, à
$x$ fixé, toutes les fonctions présentes sous une intégrable doivent être continues par morceaux et intégrables.
Une exception près les fonctions inférieures à $g$ en valeur absolue dans $(CD)$ n'ont pas besoin d'être intégrables, puisqu'elles le sont automatiquement.
- Les conditions $(CD)$ sont les conditions de domination qui permettent d'utiliser le théorème de convergence dominée.
- Sans les conditions $(*)$, les théorèmes ressemblent à :
- $f$ $C^0$ par rapport à la variable $x$ et condition de domination implique $F$ $C^0$ $($par rapport à la variable $x)$.
- $f$ $C^1$ par rapport à la variable $x$ et condition de domination implique $F$ $C^1$ $($par rapport à la variable $x)$.
- La fonction $g$ présente dans les hypothèses de domination est indépendante du paramètre $($ici $x)$ et ne dépend donc que de $t$.
Exercice - intégrale de Gauss.14
Soit $F$ la fonction définie sur $[0;+\infty[$ par :
$$F(x)\=\int_0^1\frac{e^{-x(1+t^2)}}{1+t^2}dt$$
- Montrer que $F$ est dérivable et calculer $F'$.
- Calculer $F(0)$ et $\limite{x}{+\infty}F(x)$.
- Posons $g(x)=F(x^2)$. Calculer $g'$ puis en déduire que :
$$g(x)\:+\:\left(\int_0^xe^{-t^2dt}\right)^2\=\frac{\pi}{4}$$
- En déduire que : $$\int_0^{+\infty}e^{-t^2}dt\=\frac{\sqrt{\pi}}{2}$$
|
II. Paramètre réel dans l'intégrale.
II.4. Caractère $C^p$.
Théorème.15
Soit $p$ dans $\SetN$. Avec les notations de $f$ et $F$ de début de paragraphe, si pour tout segment $[a,b]$, il existe une fonction $g$ dans $\mathcal{C}_m(I,\SetR^+)$ telles que :
$$\left\{\begin{array} {ll}%
x\mapsto f(x,t)\hbox{ est de classe $C^p$ pour tout $t$ de $I$}\\
\Haut{0.6}\forall j\in[\![0,p]\!],\:\forall x\in D,\:t\mapsto \frac{\delta^j f}{\delta x^j}(x,t)\hbox{ continue par morceaux.}&^{(*)}\\
\Haut{0.6}\forall j\in[\![0,p-1]\!],\:\forall x\in D,\:t\mapsto \frac{\delta^j f}{\delta x^j}(x,t)\hbox{ intégrable.}&^{(*)}\\
\Haut{0.6}\forall x\in[a,b]\subset D,\:\:\left|\frac{\delta^p f}{\delta x^p}(x,t)\right|\:\leq\: g(t)&^{(CD)}\\
\Haut{0.6}g\hbox{ intégrable sur }I&^{(CD)}\\
\end{array}%
\right.$$
alors $F$ est de classe $C^p$ sur $D$ et $F^{(p)}(x)\=\ds\int_{I}\hbox{$\frac{\delta^p f}{\delta x^p}$}(x,t)dt$
Remarque.
- En pratique, comme dans les deux théorèmes précédents, on vérifie l'hypothèse de domination sur tout segment de $D$ $($ou tout autre intervalle adapté à la situation$)$.
- Si $p=0$ ou si $p=1$, on retrouve les deux théorèmes du paragraphe précédent.
- Si on veut montrer que la fonction $F$ est $C^\infty$, on montre qu'elle est $C^p$ pour $p$ quelconque dans $\SetN$.
Exercice - théorème de division.16
Soit $f$ une application de $C^\infty(\SetR,\SetR)$ vérifiant $f(0)=0$. Notons $g$ la fonction $\frac{f(x)}{x}$ prolongée par continuité en 0.
- Que vaut $g(0)$ ? Montrer que $f^{(n+1)}$ est bornée sur $[-1;1]$ pour tout $n$ de $\SetN$.
- Montrer que $\ds g(x)=\int_0^1f'(xt)dt$
- Montrer que $\:g\:$ est $C^\infty$ sur $[-1;1]$, puis sur $\SetR$.
|
II. Paramètre réel dans l'intégrale.
II.5. Fonction Gamma d'Euler.
Exercice - La fonction Gamma.17
La fonction gamma d'Euler est définie par :
$$\Gamma(x)\=\int_0^{+\infty}e^{-t}t^{x-1}dt$$
On notera $f(x,t)=e^{-t}t^{x-1}$
- Montrer que, pout tout $p$ de $\SetN$, l'intégrale :
$$I_p(x)\=\int_0^{+\infty}\ln^p(t)e^{-t}t^{x-1}dt$$
est absolument convergente pour $x$ dans $\SetR^*_+$. En déduire que $\Gamma$ est définie sur $\SetR^*_+$.
- Soit $[a,b]$ un segment de $\SetR^*_+$. Montrer que :
$$\forall x\in[a,b],\:\forall t\in]0;+\infty[,\:\:\:t^{x-1}\:\leq\:t^{a-1}+t^{b-1}$$
- Montrer que $\Gamma$ est $C^{\infty}$ sur $\SetR^*_+$. Que vaut $\Gamma^{(p)}$ pour $p$ dans $\SetN$ ?
- Montrer que : $\forall x\in\SetR^+,\:\Gamma(x+1)\=x\Gamma(x)$. En déduire que la fonction $\Gamma$ prolonge la factorielle c'est-à-dire que : $$\forall n\in\SetN,\:\Gamma(n+1)=n!$$
- Montrer que $\ds\Gamma(x)\:\mathop{\sim}_0\:\frac{1}{x}$. Tracer la courbe.
|