$$
\newcommand{\SetN}{\mathbb{N}}
\newcommand{\SetR}{\mathbb{R}}
\newcommand{\SetC}{\mathbb{C}}
\newcommand{\SetK}{\mathbb{K}}
\newcommand{\SetZ}{\mathbb{Z}}
\newcommand{\SetQ}{\mathbb{Q}}
\newcommand{\SetU}{\mathbb{U}}
\newcommand\ds[0]{\displaystyle}
\newcommand\PCar[1]{\large{\chi}_{#1}}
\newcommand{\=}{\:=\:}
\newcommand\tendvers[2]{\displaystyle\mathop{\longrightarrow}_{#1\rightarrow#2}}
\newcommand\tr[0]{\:^t\!}
\newcommand\limite[2]{\displaystyle\mathop{\text{lim}}_{#1\rightarrow#2}\:}
\newcommand\Sup[1]{\displaystyle\mathop{sup}_{#1}}
\newcommand\Inf[1]{\displaystyle\mathop{inf}_{#1}}
\newcommand\Haut[1]{}
\newcommand\vect[1]{\overrightarrow{#1}}
\newcommand\tendversCU[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CU}}\:}
\newcommand\tendversCS[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CS}}\:}
\newcommand\tendversCN[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CN}}\:}
\newcommand\tendversCUS[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CUS}}\:}
\newcommand\tendversNorme[1]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{#1}\:}
\newcommand\simL[0]{\displaystyle\mathop{\sim}_{^{^L}}}
\newcommand\simC[0]{\displaystyle\mathop{\sim}_{^{^C}}}
\newcommand\simLC[0]{\displaystyle\mathop{\sim}_{^{^{LC}}}}
\newcommand\fonction[5]{
\begin{array}{cccc}
#1\::\:& #2 & \rightarrow & #3 \\
& #4 & \mapsto & \ds #5 \
\end{array}}
$$
| Liste chapitres |
Plan du chapitre |
 | Section |  |
|
 | sous-section |  |
|
|
|
| Ici sera la liste des chapitres !!! |
|
I. Paramètre entier dans l'intégrale.
I.1. Problématique
Que cherche-t-on à faire ?
On va chercher des hypothèses suffisantes pour pouvoir intervertir les symboles $\lim$ et $\int$, c'est-à-dire quelles conditions doit-on avoir sur une suite d'applications $(f_n)$ définies d'un intervalle $I$ de $\SetR$ dans $\SetK$ pour avoir $$\limite{n}{+\infty}\int_{I}f_n\=\int_{I}\limite{n}{+\infty}f_n$$
Le contre-exemple suivant montre que la question est pertinente puisqu'il existe des cas où l'inversion est impossible :
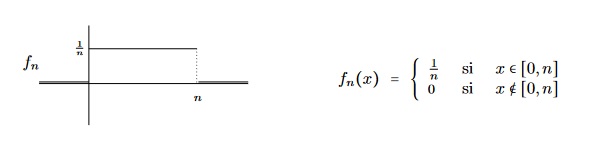
On a donc et $\:\:\:f_n\tendversCU 0\:\:$, $\:\limite{n}{+\infty}\int_{0}^{+\infty}f_n\=1\:$ et $\:\ds\int_{0}^{+\infty}\limite{n}{+\infty}f_n\=0\:$.
|
I. Paramètre entier dans l'intégrale.
I.2. Rappel : le cas d'une CU sur un segment.
Théorème - version suite.1
Si $(f_n)$ est une suite d'applications continues définies d'un segment $[a,b]$ de $\SetR$ dans $\SetK$ convergeant uniformément alors :
$$\limite{n}{+\infty}\int_a^bf_n\=\int_a^b\limite{n}{+\infty}f_n$$
Théorème - version série.2
Si $\sum f_n$ est une série d'applications continues définies d'un segment $[a,b]$ de $\SetR$ dans $\SetK$ convergeant uniformément alors
$$\sum_{n=0}^{+\infty}\int_a^bf_n\=\int_a^b\sum_{n=0}^{+\infty}f_n$$
Ce théorème est appelé "Théorème d'intégration terme à terme - version CU sur un segment".
Remarque.
Ce théorème est un rappel. Voir toutes les informations sur ce théorème et les exemples dans le chapitre suite de fonctions.
|
I. Paramètre entier dans l'intégrale.
I.3. Théorème de convergence dominée.
Théorème.3
Soient $f$ et $f_n$ des application de $I$ dans $\SetK$ pour tout $n$ de $\SetN$, alors :
$$
\exists g\in\mathcal{C}_m(I,\SetR^+),\:\:\left\{\begin{array} {ll}%
f_n\tendversCS f&\\
\text{Les }f_n\text{ et }f\text{ sont continues par morceaux }&^{(*)}\\[0.15cm]
\:g\:\hbox{ intégrable sur }I&^{(CD)}\\[0.15cm]
\:\forall n\in\SetN,\:|f_n|\leq g &^{(CD)}\\
\end{array}%
\right.
$$
alors les $f_n$ et $f$ sont intégrables et $\ds\int_{_I}\limite{n}{+\infty}f_n\=\limite{n}{+\infty}\int_{_I}f_n$
Remarques.
- On rappelle que $g$ intégrable sur $I$ signifie $\ds\int_{_I}|g|$ convergente et que si une fonction continue par morceaux $f$ vérifie $|f|\leq g$ avec $g$ intégrable sur $I$ alors $f$ est aussi intégrable sur $I$.
- Les hypothèses $(CD)$ sont appelées les hypothèses de domination.
- Les hypothèses $(*)$ ne sont utiles que pour donner un sens aux intégrales.
- Comme dans tout le chapitre la fonction $g$ présente dans les hypothèses de domination est indépendante du paramètre (ici $n$) et ne dépend donc que de $t$.
Exercice.4
Déterminer la limite des intégrales suivantes :
$$
I_n=\ds\int_0^{\frac{\pi}{2}}\sin^n(t)dt\hskip2.2cm
J_n=\ds\int_0^{+\infty}\frac{1}{{(1+t^2)}^n}dt\hskip2.2cm
K_n=\ds\int_0^{+\infty}\frac{1}{1+t^2+t^n}dt
$$
Exercice - Qui c'est le plus fort ? 5
Le but de cet exercice est de montrer que le théorème de convergence dominée est plus efficace que le théorème d’interversion limite-intégrale version convergence uniforme sur un segment. Pour cela, on va démontrer ce dernier théorème à l'aide du théorème de convergence dominée.
Soit $(f_n)$ une suite de fonctions continues sur le segment $[a,b]$ de $\SetR$ convergeant uniformément vers une fonction $f$.
- Montrer qu'il existe $M$ dans $\SetR$ tel que :
$$\forall n\in\SetN,\:\forall x\in[a,b],\:\:|f_n(x)|\leq M$$
- Montrer à l'aide du théorème de convergence dominé que :
$$\limite{n}{+\infty}\int_a^bf_n\=\int_a^b\limite{n}{+\infty}f_n$$
|
I. Paramètre entier dans l'intégrale.
I.4. Intégration terme à terme.
Remarque.
Dans le cas des séries, on peut très bien utiliser le théorème de convergence dominée tel quel. Cependant, il est souvent plus utile d'utiliser la version suivante qui est une conséquence du théorème de convergence dominée. Il a l'avantage de ne pas avoir à trouver une fonction $g$. On l'appelle le "théorème d'intégration terme à terme - version convergence dominée".
Théorème.6
Soient $f$, $f_n$ des applications de $I$ dans $\SetK$ $(n\in\SetN)$, alors :
$$\left\{\begin{array} {l}%
\sum f_n\tendversCS f\\[0.15cm]
\text{Les }f_n\text{ et }f\text{ sont continues par morceaux }^{(*)}\\[0.15cm]
\Haut{0.6}\hbox{Les intégrales }\ds\int_{_I}|f_n|\:\:\hbox{ sont convergentes pour tout }n\\
\Haut{0.6}\hbox{La série }\ds\sum \int_{_I}|f_n|\hbox{ est convergente}
\end{array}%
\right.\hskip0.5cm\Longrightarrow\hskip0.5cm\left\{\begin{array} {l}%
\:\:f\hbox{ intégrable}\\
\Haut{0.8}\ds\int_{_I}f\=\sum_{n=0}^{+\infty}\int_{_I}f_n\\
\end{array}
\right.$$
Remarques.
-
Contrairement au théorème de convergence dominée, on demande aux $f_n$ d'être intégrables.
- Les hypothèses $(*)$ ne sont utiles que pour donner un sens aux intégrales.
- Puisque ce théorème se démontre à l'aide du théorème de convergence dominée, il est donc moins puissant que celui-ci quoique plus simple à utiliser. L'exercice suivant montre cependant qu'on est parfois obligé de revenir au théorème de convergence dominée.
Exercice.7
Pour tout $n$ de $\SetN$ et tout $x$ de $[0,1]$, on pose :
$f_n(x)\=(-x^2)^n$.
On cherche à savoir si :
$$\sum_{n=0}^{\infty}\int_0^{1}\!\!\!f_n\=\int_0^{1}\!\sum_{n=0}^{\infty}f_n$$
- Montrer que $\ds\sum\int_0^{1}\:\:|f_n|$ est divergente. En déduire qu'on ne peut pas appliquer le théorème d'intégration terme à terme.
- Montrer que pour tout $N$ de $\SetN$, on a :
$$\forall x\in[0,1],\:\:\left|\sum_{n=0}^{N}f_n(x)\right|\:\:\leq\:\:2$$
- En déduire que l'on peut utiliser le théorème de convergence dominée, et que l'on a :
$$\sum_{n=0}^\infty\frac{(-1)^n}{2n+1}\:\=\:\frac{\pi}{4}$$
Exercice.8
- Montrer que :
$$\sum_{k=0}^{+\infty}\int_0^1x^{2n}(1-x)dx\=\int_0^1\frac{1}{1+x}dx$$
- En déduire que :
$$\sum_{k=1}^{+\infty}\frac{(-1)^{k+1}}{k}\=\ln(2)$$
|
I. Paramètre entier dans l'intégrale.
I.5. Application au calcul d'intégrales.
Remarque.
Comme le montre l'exemple suivant, pour calculer une intégrale, il est parfois judicieux de faire apparaitre une série de fonction et d'intervertir les symbole $\int$ et $\sum$.
Exercice.9
En faisant apparaitre une série géométrique, montrer que : $$\int_0^{+\infty}\frac{t}{e^t-1}dt\=\frac{\pi^2}{6}$$
|