Psi - Math - Lycée Alphone Daudet

Liste chapitres

Plan du chapitre

Section

sous-section

III. Interversion de limites.

III.1. Interversion limite-intégrale.

Théorème.^²¹

Soit $(f_n)$ une suite de fonctions continues définies sur le segment $[a,b]$. $$ f_n\tendversCU f \hskip0.9cm\Longrightarrow\hskip0.9cm \limite{n}{+\infty}\int_a^bf_n\=\int_a^b\limite{n}{+\infty}f_n\=\int_a^bf $$

Remarques.^²²

On suppose les fonctions $f_n$ continues pour avoir automatiquement $f$ continue grâce au théorème de conservation de la continuité par CU. On est ainsi sûr que $\int_a^b f$ a un sens. On peut très bien supposer les $f_n$ juste continues par morceaux, mais dans ce cas il faut :
- Soit améliorer notre construction de l'intégrale pour donner un sens aux intégrales des limites des fonctions continues par morceaux $($cad les fonctions réglées$)$. Ça existe, mais c'est hors programme.
- Soit remplacer l'hypothèse $f_n$ continues par $f_n$ continues par morceaux et $f$ continue par morceaux.
Le programme propose le théorème qui est dans l'encadré.
Le théorème est faux si l'intégrale n'est pas sur un segment. Prendre $$f_n(x)=\left\{\begin{array} {lll}% \frac{1}{n}&\hbox{si}&x\in[0,n]\\ \Haut{0.5}0&\hbox{si}&x\in[n,+\infty[\\ \end{array}\right.% $$
Le théorème est faux s'il n'y a pas convergence uniforme. Prendre pour $n\geq 2$ la suite de fonctions $(f_n)$ définie sur $\SetR^+$ par : $$f_n(x)=\left\{\begin{array} {ccc}% n^2x&\hbox{si}&x\in\left[0;\frac{1}{n}\right]\\ \Haut{0.5}2n-n^2x&\hbox{si}&x\in\left[\frac{1}{n};\frac{2}{n}\right]\\ \Haut{0.5}0&\hbox{si}&x\in\left[\frac{2}{n};1\right]\\ \end{array}% \right.$$
Reformulation dans le cadre des séries de fonctions. Le théorème est alors appelé intégration termes à termes. Soit $(f_n)$ une suite de fonctions continues définies sur le segment $[a,b]$ telle que la série $\sum f_n$ converge uniformément alors $$ \int_a^b\sum_{n=0}^{+\infty}f_n\:\=\:\sum_{n=0}^{+\infty}\int_a^bf_n $$

Exercice - théorème des moments.^²³

Soit $f$ une fonction continue sur $[a,b]$ vérifiant : $$\forall P\in\SetR[X],\:\:\int_a^bf(t)P(t)dt\=0$$

Montrer en utilisant le théorème de Bernstein que : $\ds\int_a^bf^2=0$.
En déduire que $\:\SetR[X]^\perp=\{0\}\:$ dans l'espace pré-hilbertien $\mathcal{C}([a,b],\SetR)$

Exercice.^²⁴

Soient $n$ et $p$ dans $\SetN$. Montrer que l'intégrale suivante est convergente, puis la calculer : $$I_{pn} \=\int_0^1x^p\ln^n(x)dx$$
Pour tout $n$ de $\SetN^*$, notons $f_n$ l'application de $[0,1]$ dans $\SetR$ définie par : $$f_n(x)=\left\{\begin{array} {ccc}% x^n\ln^n(x)&\text{si }x>0\\ 0&\text{si }x=0\\ \end{array}% \right.$$ On note également $f_0=1$. Montrer que pour tout $n$ de $\SetN$, l'application $f_n$ est continue et bornée par 1.
Pour tout $x$ de $[0,1]$, notons : $$f(x) = \sum_{n=0}^{+\infty}\frac{(-1)^nf_n(x)}{n!}$$ Montrer que la convergence définissant $f$ est uniforme.
En déduire que : $$\int_0^1\frac{1}{x^x}\=\sum_{n=1}^\infty\frac{1}{n^n}$$

III. Interversion de limites.

III.3. Interversion limite-limite.

Théorème de la double limite.^²⁸

Soit $(f_n)$ une suite $($ou une série$)$ de fonctions de $I$ dans $\SetK$ et $a$ une extrémité de $I$. Si $$\left\{% \begin{array} {l}% f_n\tendversCU f\\ \Haut{0.5}f_n(x)\tendvers{x}{a}l_n \end{array}% \right.\hskip0.5cm\Longrightarrow\hskip0.5cm \limite{n}{+\infty}l_n \hbox{ et } \limite{x}{a}f(x) \hbox{ existent et sont égales.} $$ On peut résumer la situation sur le schéma suivant :

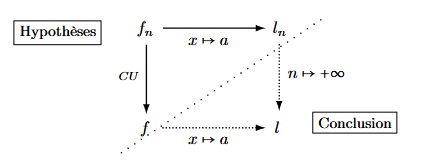Sous forme condensée, on peut écrire : $$\limite{x}{a}\limite{n}{+\infty}f_n(x)\=\limite{n}{+\infty}\limite{x}{a}f_n(x)$$

Exercice.^²⁹

Montrer que : $$\sum_{k=1}^{+\infty}\frac{(-1)^{k-1}}{k}\=\ln(2)$$

En utilisant le théorème de la double limite et que sur $[0,1[$ : $$\ds\ln(1+x)\=\sum_{k=1}^{+\infty}\frac{(-1)^{k-1}x^{k}}{k}$$
Sans utiliser le théorème de la double limite et en intégrant la somme $\ds\sum_{k=0}^n(-x)^k$.