 |
Cours Suites et séries de fonctions. |
|
$$
\newcommand{\SetN}{\mathbb{N}}
\newcommand{\SetR}{\mathbb{R}}
\newcommand{\SetC}{\mathbb{C}}
\newcommand{\SetK}{\mathbb{K}}
\newcommand{\SetZ}{\mathbb{Z}}
\newcommand{\SetQ}{\mathbb{Q}}
\newcommand{\SetU}{\mathbb{U}}
\newcommand\ds[0]{\displaystyle}
\newcommand\PCar[1]{\large{\chi}_{#1}}
\newcommand{\=}{\:=\:}
\newcommand\tendvers[2]{\displaystyle\mathop{\longrightarrow}_{#1\rightarrow#2}}
\newcommand\tr[0]{\:^t\!}
\newcommand\limite[2]{\displaystyle\mathop{\text{lim}}_{#1\rightarrow#2}\:}
\newcommand\Sup[1]{\displaystyle\mathop{sup}_{#1}}
\newcommand\Inf[1]{\displaystyle\mathop{inf}_{#1}}
\newcommand\Haut[1]{}
\newcommand\vect[1]{\overrightarrow{#1}}
\newcommand\tendversCU[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CU}}\:}
\newcommand\tendversCS[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CS}}\:}
\newcommand\tendversCN[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CN}}\:}
\newcommand\tendversCUS[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CUS}}\:}
\newcommand\tendversNorme[1]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{#1}\:}
\newcommand\simL[0]{\displaystyle\mathop{\sim}_{^{^L}}}
\newcommand\simC[0]{\displaystyle\mathop{\sim}_{^{^C}}}
\newcommand\simLC[0]{\displaystyle\mathop{\sim}_{^{^{LC}}}}
\newcommand\fonction[5]{
\begin{array}{cccc}
#1\::\:& #2 & \rightarrow & #3 \\
& #4 & \mapsto & \ds #5 \
\end{array}}
$$
| Liste chapitres | Plan du chapitre |
|
|
||||||
| |||||||||
| |||||||||
I. Modes de convergence. I.1. A propos de la norme infinie.
Définition.
Soit $f$ dans $\mathcal{F}(I,\SetR)$ et $A\subset I$. On note :
$${\|f\|}_\infty^{^A} \:\=\:\mathop{\text{Sup}}_{x\in A}\:|f(x)|$$
Comme le sup n'est pas toujours fini, ${\|f\|}_\infty^{^A}$ peut éventuellement valoir $+\infty$. C'est donc un élément de $\overline{\SetR^+}=\SetR^+\cup\{+\infty\}$.
S'il n'y a pas d'ambiguïté sur $A$, on notera simplement ${\|f\|}_\infty$.
Remarques.
Soit $I$ un intervalle de $\SetR$. On rappelle que :
Propriétés.1
Les propriétés ressemblent à celle d'une norme :
Définition.
Soit $(f_n)$ une suite de fonctions et $l$ dans $\SetR$, alors $\:\:\|f_n\|_{\infty}\tendvers{n}{+\infty}l\:\:$ signifie que :
$$\forall\varepsilon\in\SetR^*_+,\:\exists N\in\SetN,\:\forall n\geq N,\:\:\:\Big|\|f_n\|_{\infty}-l\Big|\leq\varepsilon$$
C'est la même définition que les suites dans $\SetR$. En d'autres termes $\:\:\|f_n\|_{\infty}\:\:$ est finie à partir d'un certain rang et que la suite de réels $\:\:\|f_n\|_{\infty}\:\:$ à partir de ce rang tend vers 0.
| |||||||||
I. Modes de convergence. I.2. Convergence simple, convergence uniforme.
Définitions.
Soient $f_n$ et $f$ dans $\mathcal{F}(I,\SetR)$ avec $I$ un intervalle de $\SetR$.
Remarques.
Propriétés - traduction epsilonnesque.2
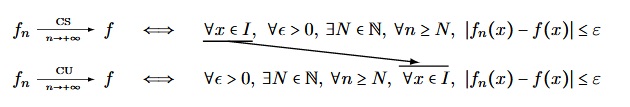 Ainsi, dans la cas de la convergence uniforme, le $N$ choisi doit convenir à tous les $x$ de $I$. Dans la convergence simple, on choisit un $N$ pour chaque $x$.
Vision géométrique de la convergence uniforme.
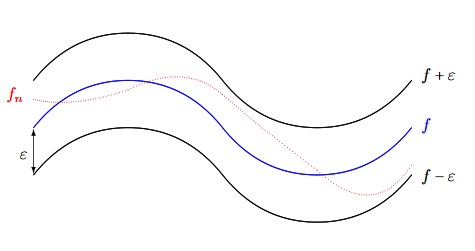 La suite $(f_n)$ converge uniformément vers $f$, si et seulement si, pour tout $\varepsilon$ strictement positif, les graphes des fonctions $f_n$ sont entre les 2 courbes noires APCR. | |||||||||
I. Modes de convergence. I.3. Relations entre les types de convergence.
Théorème.3
$$f_n\tendversCU f\hskip1cm\Longrightarrow\hskip1cm f_n\tendversCUS f\hskip1cm\Longrightarrow\hskip1cm f_n\tendversCS f$$
Contre-exemple 1.
Il peut y avoir convergence simple et pas convergence uniforme $($ni uniformément sur tout segment$)$ comme le montre l'exemple suivant. Considérons la suite de fonction $(f_n)$ définie sur $\SetR^+$ par :
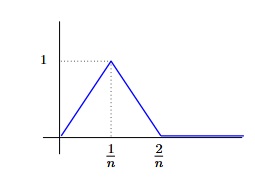 La suite $(f_n)$ convergence simplement vers la fonction nulle mais ne converge pas ni uniformément ni uniformément sur tout segment.
Contre-exemple 2.
Il peut y avoir convergence uniforme sur tout segment et pas convergence uniforme. Par exemple si les fonctions du contre exemple précédent sont définies sur $\SetR^*_+$, on a convergence uniforme sur tout segment, mais toujours pas convergence uniforme.
| |||||||||
I. Modes de convergence. I.4. Exemples et plan d'étude pour les suites de fonctions.
Comment étudier un suite de fonctions $(f_n)$ ?
Exercice.4
Étudier la convergence des suites de fonctions suivantes :
$$\begin{array}{lll}
1.\:\:\ds f_n(x)=x^n\hskip0.2cm\hbox{ sur }[0,1]\hskip2cm&
2.\:\:\ds f_n(x)=x^n\hskip0.2cm\hbox{ sur }[0,1[&
3.\:\:\ds f_n(x)=\frac{x}{x+n}\hbox{ sur }\SetR^+\\[0.3cm]
4.\:\:\ds f_n(x)=\frac{\sqrt{n}x}{e^{nx}}\hbox{ sur }\SetR^+&
5.\:\:\ds f_n(x)=\frac{n(x^2-4)}{1+n(x+2)}\hbox{ sur }[-2;2]
\end{array}$$
| |||||||||
I. Modes de convergence. I.5. Séries de fonctions.
Remarques préliminaires.
Comme une série est une suite particulière, il y a encore les trois types de convergence vus précédemment. Cependant :
Définitions.
Propriétés.5
Méthode.
La contraposée du premier point peut permettre de montrer qu'une série de fonctions ne converge pas uniformément : il suffit donc de montrer que $(f_n)$ ne converge pas uniformément vers 0.
Par exemple, la série $\sum x^n$ ne converge pas uniformément sur $[0,1[$, car $(x^n)$ ne converge pas uniformément vers 0 sur $[0,1[$.
Contre-exemple.
Il peut y avoir convergence uniforme et pas convergence normale comme le montre l'exemple suivant. Considérons la suite de fonction $(f_n)$ définie sur $\SetR^+$ par :
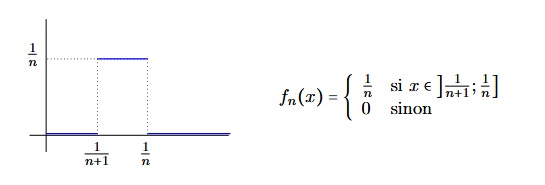 La série $\sum f_n$ converge uniformément mais pas normalement. | |||||||||
I. Modes de convergence. I.6. Exemples et plan d'étude pour les séries de fonctions.
Remarques.
La méthode est la même que celle pour les suites mise à part :
Exercice.6
Étudier les séries de fonctions de terme général $f_n$ définie par :
$$\begin{array}{lcl}
1.\:\:\ds f_n(x)=\frac{(-1)^k}{x+k}\hbox{ sur }\SetR^+&\hskip2cm&
2.\:\:\ds f_n(x)=\frac{x^{n}}{n!}\hbox{ sur }\SetR\\[0.3cm]
3.\:\:\ds f_n(x)=x^{n}(1-x)\hbox{ sur }[0,1]&&
4.\:\:\ds f_n(x)=\frac{1}{n+n^3x^2}\hbox{ sur }]0,+\infty[\\
\end{array}$$
Exercice.7
Considérons $f_n$ la fonction de $\SetR^+$ définie par le graphe suivant :

| |||||||||
I. Modes de convergence. I.7. Stabilité par combinaison linéaire, produit de fonctions bornées.
Théorème.8
Soient $\lambda$, $\mu$ dans $\SetK$ et $(S_n)$, $(T_n)$ des suites ou des séries de fonctions de $I$ dans $\SetK$, alors :
$$\left\{\begin{array} {l}%
S_n\tendversCS S\\
\Haut{0.45}T_n\tendversCS T\\
\end{array}%
\right.\hskip0.5cm\Longrightarrow\hskip0.5cm\lambda.S_n+\mu.T_n\tendversCS \lambda.S+\mu.T$$
On peut remplacer CS par CUS, CU, CN et le théorème reste vrai.
Théorème.9
Soient $(S_n)$, $(T_n)$ des suites ou des séries de fonctions de $I$ dans $\SetK$, alors :
Exercice.10
Considérons la suite de fonctions $\:\:f_n(x)=x+\frac{1}{n}\:\:$ définies sur $\SetR$.
| |||||||||

