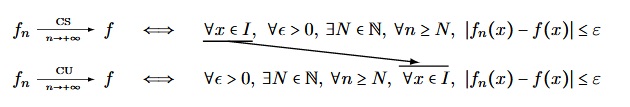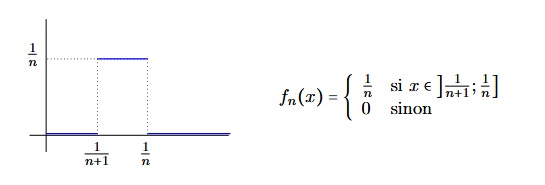$$
\newcommand{\SetN}{\mathbb{N}}
\newcommand{\SetR}{\mathbb{R}}
\newcommand{\SetC}{\mathbb{C}}
\newcommand{\SetK}{\mathbb{K}}
\newcommand{\SetZ}{\mathbb{Z}}
\newcommand{\SetQ}{\mathbb{Q}}
\newcommand{\SetU}{\mathbb{U}}
\newcommand\ds[0]{\displaystyle}
\newcommand\PCar[1]{\large{\chi}_{#1}}
\newcommand{\=}{\:=\:}
\newcommand\tendvers[2]{\displaystyle\mathop{\longrightarrow}_{#1\rightarrow#2}}
\newcommand\tr[0]{\:^t\!}
\newcommand\limite[2]{\displaystyle\mathop{\text{lim}}_{#1\rightarrow#2}\:}
\newcommand\Sup[1]{\displaystyle\mathop{sup}_{#1}}
\newcommand\Inf[1]{\displaystyle\mathop{inf}_{#1}}
\newcommand\Haut[1]{}
\newcommand\vect[1]{\overrightarrow{#1}}
\newcommand\tendversCU[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CU}}\:}
\newcommand\tendversCS[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CS}}\:}
\newcommand\tendversCN[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CN}}\:}
\newcommand\tendversCUS[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CUS}}\:}
\newcommand\tendversNorme[1]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{#1}\:}
\newcommand\simL[0]{\displaystyle\mathop{\sim}_{^{^L}}}
\newcommand\simC[0]{\displaystyle\mathop{\sim}_{^{^C}}}
\newcommand\simLC[0]{\displaystyle\mathop{\sim}_{^{^{LC}}}}
\newcommand\fonction[5]{
\begin{array}{cccc}
#1\::\:& #2 & \rightarrow & #3 \\
& #4 & \mapsto & \ds #5 \
\end{array}}
$$
| Liste chapitres |
Plan du chapitre |
 | Section |  |
|
 | sous-section |  |
|
|
|
| Ici sera la liste des chapitres !!! |
|
I. Modes de convergence.
I.1. A propos de la norme infinie.
Définition.
Soit $f$ dans $\mathcal{F}(I,\SetR)$ et $A\subset I$. On note :
$${\|f\|}_\infty^{^A} \:\=\:\mathop{\text{Sup}}_{x\in A}\:|f(x)|$$
Comme le sup n'est pas toujours fini, ${\|f\|}_\infty^{^A}$ peut éventuellement valoir $+\infty$. C'est donc un élément de $\overline{\SetR^+}=\SetR^+\cup\{+\infty\}$.
S'il n'y a pas d'ambiguïté sur $A$, on notera simplement ${\|f\|}_\infty$.
Remarques.
Soit $I$ un intervalle de $\SetR$. On rappelle que :
- ${\|.\!.\!.\|}_\infty^{_{[a,b]}}$ est une norme sur $\mathcal{C}_{pm}([a,b],\SetR)$.
- ${\|.\!.\!.\|}_\infty^{_I}$ est une norme sur $\mathcal{B}(I,\SetR)$, l'espace vectoriel des fonctions bornées de $I$ dans $\SetR$.
- ${\|.\!.\!.\|}_\infty^{_I}$ n'est pas une norme sur $\mathcal{C}(I,\SetR)$ ou sur $\mathcal{C}_{pm}(I,\SetR)$ car les fonctions ne sont pas forcément bornées et la norme infinie peut valoir $+\infty$.
Propriétés.1
Les propriétés ressemblent à celle d'une norme :
- $\|f+g\|_\infty\:\leq\: \|f\|_\infty+ \|g\|_\infty$ pour toutes fonctions $f$ et $g$.
- $\|\lambda f\|_\infty\=|\lambda|.\|f\|_\infty$ pour toute fonction $f$ et tout réel $\lambda$ non nul.
- Si $\:\|f\|_\infty=0\:$ alors $\:f=0\:$ sur $A$.
La grosse différence avec une norme est que ces égalités/inégalité sont à prendre dans $\overline{\SetR}$.
Définition.
Soit $(f_n)$ une suite de fonctions et $l$ dans $\SetR$, alors $\:\:\|f_n\|_{\infty}\tendvers{n}{+\infty}l\:\:$ signifie que :
$$\forall\varepsilon\in\SetR^*_+,\:\exists N\in\SetN,\:\forall n\geq N,\:\:\:\Big|\|f_n\|_{\infty}-l\Big|\leq\varepsilon$$
C'est la même définition que les suites dans $\SetR$. En d'autres termes $\:\:\|f_n\|_{\infty}\:\:$ est finie à partir d'un certain rang et que la suite de réels $\:\:\|f_n\|_{\infty}\:\:$ à partir de ce rang tend vers 0.
|
I. Modes de convergence.
I.2. Convergence simple, convergence uniforme.
Définitions.
Soient $f_n$ et $f$ dans $\mathcal{F}(I,\SetR)$ avec $I$ un intervalle de $\SetR$.
- La suite $(f_n)$ converge simplement vers $f$ $($on note $f_n\tendversCS f)$ ssi :
$\forall x\in I,\:\:f_n(x)\tendvers{n}{+\infty}f(x)$
- La suite $(f_n)$ converge uniformément vers $f$ $($on note $f_n\tendversCU f)$ ssi :
${\|f_n-f\|}_\infty\tendvers{n}{+\infty}0$
- La suite $(f_n)$ converge uniformément sur tout segment vers $f$ $($on note $f_n\tendversCUS f)$ ssi $(f_n)$ converge uniformément vers $f$ sur tout segment $[a,b]$ de $I$
Remarques.
- Coin de culture : la convergence simple ne provient d'aucune norme $($ni d'une distance$)$, c'est-à-dire qu'il n'existe pas de norme $N$ telle que :
$$f_n\tendversCS f\hskip1cm\Longleftrightarrow\hskip1cm f_n\tendversNorme{N}f$$
- La notion de CUS n'a pas d'intérêt si $I$ est un segment puisque dans ces cas là, elle est équivalente à la notion de CU. De plus, la notation CUS n'est pas standard. Il faut rappeler sa signification dans les copies.
- Il y a bien sûr d'autres types de convergence. La convergence avec la norme ${\|.\!.\!.\|}_1$ ou avec la nome ${\|.\!.\!.\|}_2$ par exemple. Nous n'en parlerons pas ici.
Propriétés - traduction epsilonnesque.2
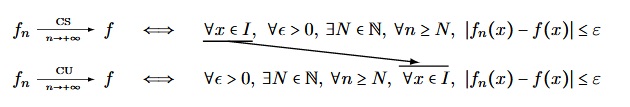
Ainsi, dans la cas de la convergence uniforme, le $N$ choisi doit convenir à tous les $x$ de $I$. Dans la convergence simple, on choisit un $N$ pour chaque $x$.
Vision géométrique de la convergence uniforme.
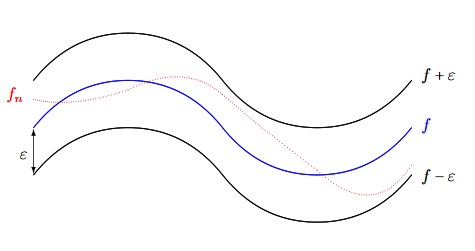
La suite $(f_n)$ converge uniformément vers $f$, si et seulement si, pour tout $\varepsilon$ strictement positif, les graphes des fonctions $f_n$ sont entre les 2 courbes noires APCR.
|
I. Modes de convergence.
I.3. Relations entre les types de convergence.
Théorème.3
$$f_n\tendversCU f\hskip1cm\Longrightarrow\hskip1cm f_n\tendversCUS f\hskip1cm\Longrightarrow\hskip1cm f_n\tendversCS f$$
Contre-exemple 1.
Il peut y avoir convergence simple et pas convergence uniforme $($ni uniformément sur tout segment$)$ comme le montre l'exemple suivant. Considérons la suite de fonction $(f_n)$ définie sur $\SetR^+$ par :
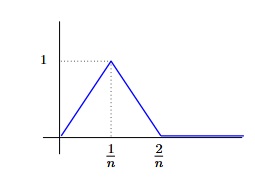
La suite $(f_n)$ convergence simplement vers la fonction nulle mais ne converge pas ni uniformément ni uniformément sur tout segment.
Contre-exemple 2.
Il peut y avoir convergence uniforme sur tout segment et pas convergence uniforme. Par exemple si les fonctions du contre exemple précédent sont définies sur $\SetR^*_+$, on a convergence uniforme sur tout segment, mais toujours pas convergence uniforme.
|
I. Modes de convergence.
I.4. Exemples et plan d'étude pour les suites de fonctions.
Comment étudier un suite de fonctions $(f_n)$ ?
- Pour chaque $x$ de $I$, on cherche $\limite{n}{+\infty}f_n(x)$. On en déduit la limite simple $f$ éventuelle.
- On étudie la fonction $f_n(x)-f(x)$.
- S'il existe une suite $(\alpha_n)$ tendant vers 0 vérifiant :
$$\forall x\in I,\:\:|f_n(x)-f(x)|\:\leq\:\alpha_n$$
alors il y a convergence uniforme $($souvent $\alpha_n=Sup|f_n(x)-f(x)|$ et est obtenu par une étude de fonction$)$
- s'il existe une suite $(x_n)$ de $I$ vérifiant :
$$\limite{n}{+\infty}\:\Big|f_n(x_n)-f(x_n)\Big|\:\neq\:0$$
alors il n'y a pas convergence uniforme. En général $x_n$ est l'abscisse du point où il y a un le maximum de la fonction $|f_n(x)-f(x)|$.
Si l'on désire la CUS, on remplace $I$ par un segment quelconque de $I$.
Exercice.4
Étudier la convergence des suites de fonctions suivantes :
$$\begin{array}{lll}
1.\:\:\ds f_n(x)=x^n\hskip0.2cm\hbox{ sur }[0,1]\hskip2cm&
2.\:\:\ds f_n(x)=x^n\hskip0.2cm\hbox{ sur }[0,1[&
3.\:\:\ds f_n(x)=\frac{x}{x+n}\hbox{ sur }\SetR^+\\[0.3cm]
4.\:\:\ds f_n(x)=\frac{\sqrt{n}x}{e^{nx}}\hbox{ sur }\SetR^+&
5.\:\:\ds f_n(x)=\frac{n(x^2-4)}{1+n(x+2)}\hbox{ sur }[-2;2]
\end{array}$$
|
I. Modes de convergence.
I.5. Séries de fonctions.
Remarques préliminaires.
Comme une série est une suite particulière, il y a encore les trois types de convergence vus précédemment. Cependant :
- Les limites des séries sont souvent plus difficiles à déterminer que les limites de suites. On se contente donc souvent de donner le type de convergence sans préciser la limite. La limite d'une série de fonctions $\sum f_n$ est alors notée $\ds\sum_{k=0}^{+\infty}f_n$.
- Ainsi l'expression $S-S_n$ lorsque $(S_n)=\sum f_n$ est une série de fonctions peut être remplacée par le reste de la série :
$$R_n(x)=\sum_{k=n+1}^{+\infty}f_k(x)$$
- Il existe un 4$^{\text{ième}}$ type de convergence : la convergence normale. On pourra commencer par étudier la convergence normale ou simple. Par contre il faudra quand même toujours étudier la convergence simple avant la convergence uniforme pour avoir l'existence du reste.
Définitions.
- Reformulation des 3 modes de convergence déjà vus :
- $\ds\sum f_k\:\:\text{CS} \hskip0.3cm\Longleftrightarrow\hskip0.3cm\forall x\in I,\:\:\sum f_n(x)$ converge
- $\ds\sum f_k\:\:\text{CU} \hskip0.3cm\Longleftrightarrow\hskip0.3cm R_n\tendversCU 0$
- $\ds\sum f_k\:\:\text{CUS} \hskip0.3cm\Longleftrightarrow\hskip0.3cmR_n\tendversCU 0 \hbox{ sur tout segement de }I$
- un autre mode de convergence : la convergence normale :
- $\ds\sum_{k=0}^nf_k\:\:\text{CN} \hskip0.3cm\Longleftrightarrow\hskip0.3cm \sum \|f_n\|_\infty\hbox{ converge}$
Propriétés.5
- $\:\:\ds \sum f_k\:\:\text{CU} \hskip0.6cm\Longrightarrow\hskip0.6cm f_n\tendversCU 0$
- $\:\:\ds\sum f_k \:\:\text{CN} \hskip0.6cm\Longrightarrow\hskip0.6cm \sum f_k \:\:\text{CU}\hskip0.6cm\Longrightarrow\hskip0.6cm \sum f_k \:\:\text{CUS}\hskip0.6cm\Longrightarrow\hskip0.6cm \sum f_k \:\:\text{CS}$
Méthode.
La contraposée du premier point peut permettre de montrer qu'une série de fonctions ne converge pas uniformément : il suffit donc de montrer que $(f_n)$ ne converge pas uniformément vers 0.
Par exemple, la série $\sum x^n$ ne converge pas uniformément sur $[0,1[$, car $(x^n)$ ne converge pas uniformément vers 0 sur $[0,1[$.
Contre-exemple.
Il peut y avoir convergence uniforme et pas convergence normale comme le montre l'exemple suivant. Considérons la suite de fonction $(f_n)$ définie sur $\SetR^+$ par :
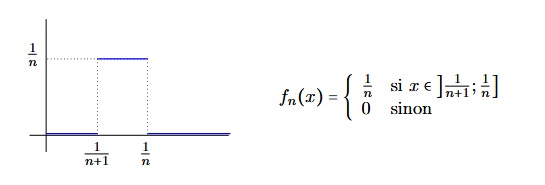
La série $\sum f_n$ converge uniformément mais pas normalement.
|
I. Modes de convergence.
I.6. Exemples et plan d'étude pour les séries de fonctions.
Remarques.
La méthode est la même que celle pour les suites mise à part :
-
que pour la CU, on montre que le reste tend uniformément vers 0,
-
qu'il faut étudier aussi étudier la CN. Pour cela il faut étudier la convergence de la série $\sum \|f_n\|_\infty$
Exercice.6
Étudier les séries de fonctions de terme général $f_n$ définie par :
$$\begin{array}{lcl}
1.\:\:\ds f_n(x)=\frac{(-1)^k}{x+k}\hbox{ sur }\SetR^+&\hskip2cm&
2.\:\:\ds f_n(x)=\frac{x^{n}}{n!}\hbox{ sur }\SetR\\[0.3cm]
3.\:\:\ds f_n(x)=x^{n}(1-x)\hbox{ sur }[0,1]&&
4.\:\:\ds f_n(x)=\frac{1}{n+n^3x^2}\hbox{ sur }]0,+\infty[\\
\end{array}$$
Exercice.7
Considérons $f_n$ la fonction de $\SetR^+$ définie par le graphe suivant :

- Montrer que la série $\sum f_n$ converge simplement. On ne cherchera pas à exprimer sa limite $f$.
- Montrer qu'il n'y a pas CU.
- Montrer que $f$ est intégrable et pourtant $f(x)$ ne tend pas ver $0$ en $+\infty$.
|
I. Modes de convergence.
I.7. Stabilité par combinaison linéaire, produit de fonctions bornées.
Théorème.8
Soient $\lambda$, $\mu$ dans $\SetK$ et $(S_n)$, $(T_n)$ des suites ou des séries de fonctions de $I$ dans $\SetK$, alors :
$$\left\{\begin{array} {l}%
S_n\tendversCS S\\
\Haut{0.45}T_n\tendversCS T\\
\end{array}%
\right.\hskip0.5cm\Longrightarrow\hskip0.5cm\lambda.S_n+\mu.T_n\tendversCS \lambda.S+\mu.T$$
On peut remplacer CS par CUS, CU, CN et le théorème reste vrai.
Théorème.9
Soient $(S_n)$, $(T_n)$ des suites ou des séries de fonctions de $I$ dans $\SetK$, alors :
-
$\ds\left\{\begin{array} {l}%
S_n\tendversCS S\\
\Haut{0.45}T_n\tendversCS T\\
\end{array}%
\right.\hskip0.5cm\Longrightarrow\hskip0.5cm S_n.T_n\tendversCS S.T$
-
$\ds\left\{\begin{array} {l}%
S_n\tendversCU S\\
\Haut{0.45}T_n\tendversCU T\\
\Haut{0.45}S,\:T\hbox{ bornées}\\
\end{array}%
\right.\hskip0.5cm\Longrightarrow\hskip0.5cm S_n.T_n\tendversCU S.T$
Exercice.10
Considérons la suite de fonctions $\:\:f_n(x)=x+\frac{1}{n}\:\:$ définies sur $\SetR$.
- Montrer que $(f_n)$ converge uniformément sur $\SetR$ vers une fonction $f$ que l'on déterminera.
- Montrer que $(f_n^2)$ ne converge pas uniformément vers $f^2$ sur $\SetR$.
- En déduire que le produit de suites de fonctions qui convergent uniformément, ne converge pas uniformément en général.
|