 |
Cours Probabilités. |
|
$$
\newcommand{\SetN}{\mathbb{N}}
\newcommand{\SetR}{\mathbb{R}}
\newcommand{\SetC}{\mathbb{C}}
\newcommand{\SetK}{\mathbb{K}}
\newcommand{\SetZ}{\mathbb{Z}}
\newcommand{\SetQ}{\mathbb{Q}}
\newcommand{\SetU}{\mathbb{U}}
\newcommand\ds[0]{\displaystyle}
\newcommand\PCar[1]{\large{\chi}_{#1}}
\newcommand{\=}{\:=\:}
\newcommand\tendvers[2]{\displaystyle\mathop{\longrightarrow}_{#1\rightarrow#2}}
\newcommand\tr[0]{\:^t\!}
\newcommand\limite[2]{\displaystyle\mathop{\text{lim}}_{#1\rightarrow#2}\:}
\newcommand\Sup[1]{\displaystyle\mathop{sup}_{#1}}
\newcommand\Inf[1]{\displaystyle\mathop{inf}_{#1}}
\newcommand\Haut[1]{}
\newcommand\vect[1]{\overrightarrow{#1}}
\newcommand\tendversCU[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CU}}\:}
\newcommand\tendversCS[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CS}}\:}
\newcommand\tendversCN[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CN}}\:}
\newcommand\tendversCUS[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CUS}}\:}
\newcommand\tendversNorme[1]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{#1}\:}
\newcommand\simL[0]{\displaystyle\mathop{\sim}_{^{^L}}}
\newcommand\simC[0]{\displaystyle\mathop{\sim}_{^{^C}}}
\newcommand\simLC[0]{\displaystyle\mathop{\sim}_{^{^{LC}}}}
\newcommand\fonction[5]{
\begin{array}{cccc}
#1\::\:& #2 & \rightarrow & #3 \\
& #4 & \mapsto & \ds #5 \
\end{array}}
$$
| Liste chapitres | Plan du chapitre |
|
|
||||||
| |||||||||
II. Probabilité conditionnelle II.1. Définition
Définition.
Soit $A$ et $B$ des événements tels que $P(B)\neq 0$. On définit la probabilité de $A$ sachant $B$, noté $P_B(A)$ ou $P(A|B)$, par :
$$P_B(A)\=P(A|B)\=\frac{P(A\cap B)}{P(B)}$$
Exemple.
On lance un dé à six faces parfaitement équilibré et on note $B$ l'événement "Le résultat est paire".
$$
{\renewcommand{\arraystretch}{1.5}
\begin{array} {|c|c|c|}%
\hline
~\hskip0.5cm A\hskip0.5cm~&~\hskip0.5cmp(A)\hskip0.5cm~&~\hskip0.5cmP(A|B)\hskip0.5cm~\\
\hline
\hline
\{1\}&1/6&0\\
\hline
\{2\}&1/6&1/3\\
\hline
\{3\}&1/6&0\\
\hline
\{4\}&1/6&1/3\\
\hline
\{5\}&1/6&0\\
\hline
\{6\}&1/6&1/3\\
\hline
\end{array}}%
$$
Proposition.9
Soit $(\Omega,\mathcal{A}, p)$ un espace probabilisé et $B$, $C$, $D$ des événements.
Exercice.10
Dans la salle des profs 60% sont des femmes ; une femme sur trois porte des lunettes et un homme sur deux
porte des lunettes : quelle est la probabilité pour qu'un porteur de lunettes pris au hasard soit une femme ?
| |||||||||
II. Probabilité conditionnelle II.2. Présentation sous forme d'arbre 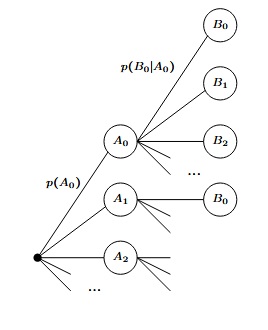 Sur les noeuds de la première colonne apparait le premier SCDE $(A_i)_{_{i\in\SetN}}$. Sur la deuxième colonne apparait le deuxième SCDE $(B_i)_{_{i\in\SetN}}$ répété autant de fois qu'il y a d'éléments dans le premier SCDE. Sur les flèches reliant la racine à un $A_i$, on indique la probabilité $p(A_i)$ et sur les flèches reliant un $A_i$ à un $B_j$, on inscrit la probabilité de $B_j$ sachant $A_i$. Pour avoir $p(A_i\cap B_j)$, on multiplie les probabilités rencontrées sur le chemin : $$Racine\:\:\longrightarrow\:\: A_i\:\:\longrightarrow\:\:B_j$$
Exercice.11
On lance une pièce bien équilibrée deux fois de suite. Présenter la situation sous forme d'arbre.
| |||||||||
II. Probabilité conditionnelle II.3. Principe des probabilités totales
Théorème.12
Soit $(A_i)_{i\in I}$ un SCDE indexé par un ensemble $I$ au plus dénombrable et $B$ un événement. On a alors :
$$P(B)\=\sum_{i\in I}P(B|A_i)P(A_i)$$
On admet que l'ordre dans lequel sont sommés les termes de la somme précédente n'influence pas la valeur de cette somme. Plus de détails dans le chapitre 'variables aléatoires'.
Convention.
On convient que dans le cas où $P(A_i)=0$, on a : $P(B|A_i)P(A_i)=0$. On peut donc utiliser le théorème des probabilités totales même avec des événements $A_i$ de probabilité nulle. Cependant il parait tout aussi naturel de les enlever de la famille $(A_i)$ puisqu'il n'interviennent pas dans la somme. On peut donc utiliser le théorème des probabilités totales avec un SQCDE au lieu d'un SCDE.
Remarques.
Dans une présentation sous forme d'arbre à 2 colonnes, le théorème des probabilités totales indique que pour trouver la probabilité d'un évènement $B$ se trouvant dans la 2$^\text{ième}$ colonne, il suffit :
Exercice.13
On dispose de 2 dés à 6 faces, un parfaitement équilibré et un faisant 6 systématiquement. On choisit un dé au hasard, puis on le lance. Quelle est la probabilité de faire 6 ?
| |||||||||
II. Probabilité conditionnelle II.4. Formule de Bayes
Théorème.14
Soient $A$ et $B$ des événements de probabilités non nulles. On a alors :
$$P(A|B)\=\frac{P(B|A)P(A)}{P(B)}$$
Conséquences.15
En combinant, la formule de Bayes avec la formule des probabilités totales, on obtient,
pour un SCDE $(A_i)_{i\in\SetN}$ de probabilités non nulles et un évènement $B$ de probabilité non nulle :
$$P(A_i|B)\=\frac{P(B|A_i)P(A_i)}{P(B)}\=\frac{P(B|A_i)P(A_i)}{\ds\:\:\:\:\sum_{k=0}^{+\infty}P(B|A_k)P(A_k)\:\:\:\:}$$
Exercice.16
On dispose de 2 dés à 6 faces, un parfaitement équilibré et un faisant 6 systématiquement. On choisit un dé au hasard, puis on le lance. On obtient 6. Quelle est la probabilité d'avoir choisi le dé pipé ?
Exercice.17
On cherche un objet dans un meuble constitué de sept tiroirs. La probabilité qu'il
soit effectivement dans ce meuble est $p$. Sachant qu'on a examiné les six
premiers tiroirs sans succès, quelle est la probabilité qu'il soit
dans le septième ?
| |||||||||
II. Probabilité conditionnelle II.5. Événements indépendants
Définitions.
Remarques.
Exercice.18
Considérons un univers à 12 éléments muni de la probabilité uniforme et les évènements $A$, $B$ et $C$ suivants :
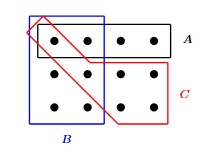
Exercice.19
On lance deux dés équilibrés à 6 faces. Montrer que les deux événements suivants sont indépendants :
Exercice.20
| |||||||||
II. Probabilité conditionnelle II.6. Indépendance et probabilité conditionnelle.
Proposition.21
A condition que les probabilités conditionnelles suivantes aient un sens,
Remarques.
| |||||||||


