$$
\newcommand{\SetN}{\mathbb{N}}
\newcommand{\SetR}{\mathbb{R}}
\newcommand{\SetC}{\mathbb{C}}
\newcommand{\SetK}{\mathbb{K}}
\newcommand{\SetZ}{\mathbb{Z}}
\newcommand{\SetQ}{\mathbb{Q}}
\newcommand{\SetU}{\mathbb{U}}
\newcommand\ds[0]{\displaystyle}
\newcommand\PCar[1]{\large{\chi}_{#1}}
\newcommand{\=}{\:=\:}
\newcommand\tendvers[2]{\displaystyle\mathop{\longrightarrow}_{#1\rightarrow#2}}
\newcommand\tr[0]{\:^t\!}
\newcommand\limite[2]{\displaystyle\mathop{\text{lim}}_{#1\rightarrow#2}\:}
\newcommand\Sup[1]{\displaystyle\mathop{sup}_{#1}}
\newcommand\Inf[1]{\displaystyle\mathop{inf}_{#1}}
\newcommand\Haut[1]{}
\newcommand\vect[1]{\overrightarrow{#1}}
\newcommand\tendversCU[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CU}}\:}
\newcommand\tendversCS[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CS}}\:}
\newcommand\tendversCN[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CN}}\:}
\newcommand\tendversCUS[0]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{_{CUS}}\:}
\newcommand\tendversNorme[1]{\:\displaystyle\mathop{\Large\longrightarrow}_{n\rightarrow+\infty}^{#1}\:}
\newcommand\simL[0]{\displaystyle\mathop{\sim}_{^{^L}}}
\newcommand\simC[0]{\displaystyle\mathop{\sim}_{^{^C}}}
\newcommand\simLC[0]{\displaystyle\mathop{\sim}_{^{^{LC}}}}
\newcommand\fonction[5]{
\begin{array}{cccc}
#1\::\:& #2 & \rightarrow & #3 \\
& #4 & \mapsto & \ds #5 \
\end{array}}
$$
| Liste chapitres |
Plan du chapitre |
 | Section |  |
|
 | sous-section |  |
|
|
|
| Ici sera la liste des chapitres !!! |
|
V. Limite et continuité.
V.1. Limite d'une suite
Définition.
Soit $E$ un espace vectoriel préhilbertien réel et $\|.\!.\!.\|$ la norme euclidienne associée.
La suite $(u_n)$ tend vers un vecteur $l$ de $E$, et on note $\:u_n\tendvers{n}{+\infty}l\:$, si et seulement si :
$$\forall\varepsilon\in\SetR^*_+,\:\exists N\in\SetN,\forall n\geq N,\:\|u_n-l\|\leq\varepsilon$$
C'est la définition de la limite d'une suite réelle en remplaçant la valeur absolue par la norme euclidienne.
Caractérisation.46
On peut toujours se ramener à la convergence d'une suite réelle puisque :
$$u_n\tendversNorme{\|\:\:\|}l\:\:\:\:\:\:\:\:\Longleftrightarrow\:\:\:\:\:\:\:\:\|u_n-l\|\tendvers{n}{+\infty}0$$
Théorème.47
- Une suite $(M_n)$ de $\mathcal{M}_{pq}(\SetR)$ tend vers $M$ si et seulement si les coefficients de $(M_n)$ tendent vers les coefficients de $M$.
- Une suite $(x_n)$ de $\SetR^n$ tend vers $x$ si et seulement si les coordonnées de $x_n$ tendent vers les coordonnées de $x$.
- Soient $(M_n)$ et $(N_n)$ des suites respectives de $\mathcal{M}_{pq}(\SetR)$ et $\mathcal{M}_{qr}(\SetR)$, alors :
$$\left\{\begin{array}{ll}
M_n\tendvers{n}{+\infty}{M}\\
N_n\tendvers{n}{+\infty}{N}\\
\end{array}\right.
\hskip1cm\Longrightarrow\hskip1cm M_nN_n\tendvers{n}{+\infty}{MN}\\
$$
Exemples.
$$n\left(\begin{array} {ccc}%
\arctan\left(\frac{1}{n}\right)\\
\cos\left(\frac{1}{n}\right)-1\\
\end{array}%
\right)\:\:\tendvers{n}{+\infty}\:\:\left(\begin{array} {ccc}%
1\\
0
\end{array}%
\right)
\hskip2cm
\frac{1}{n}\left(\begin{array} {ccc}%
(-1)^n&n+1\\
\Haut{0.48}n^2\sin\left(\frac{1}{n}\right)&1
\end{array}%
\right)\:\:\tendvers{n}{+\infty}\:\:\left(\begin{array} {ccc}%
0&1\\
\Haut{0.48}1&0
\end{array}%
\right)$$
Exercice.48
- Soit $\|.\!.\|_2$ la norme euclidienne de $\mathcal{M}_p(\SetR)$. Montrer que :
$$\forall A,B\in\mathcal{M}_p(\SetR),\:\:{\|AB\|}_2\:\leq\:{\|A\|}_2{\|B\|}_2$$
- Notons $(a_{ii}^k)$ les coefficients de la matrice $A^k$. Montrer que :
$$\forall i,j\in\{1,..., p\},\forall k\in\SetN,\:|a_{ij}^k[\:\leq\:{\|A\|}_2^k$$
- On définit l'exponentielle complexe par :
$$\forall A\in\mathcal{M}_p(\SetR),\:\:e^A\:\=\:\sum_{n=0}^\infty\frac{A^n}{n!}$$
Montrer que cette série converge.
- Comment calculer l'exponentielle d'une matrice diagonalisable $A$ de $\mathcal{M}_n(\SetR)$ ?
|
V. Limite et continuité.
V.2. Quand une notion vous manque... Suites de Cauchy $($HP$)$.
Définition.
Soit $(E,\|.\!.\!.\|)$ un espace vectoriel normé.
- Une suite $(x_n)$ est une suite de Cauchy si et seulement si :
$$\forall\varepsilon>0,\:\exists N\in\SetN,\:\forall p,q\geq N, \:\:\|x_p-x_q\|\leq\varepsilon$$
Ainsi, une suite de Cauchy est une suite qui ne "bouge" plus beaucoup à partir d'un certain rang.
- On remarquera que les suites convergentes sont des suites de Cauchy. Si la réciproque est vraie, c'est-à-dire que toutes les suites de Cauchy de $E$ convergent alors $E$ est dit complet.
- Un espace de Hilbert réel est un préhilbertien réel complet.
Exercice - une suite de Cauchy non convergente.49
Soit $E=C^0([0,1],\SetR)$ muni de son produit scalaire usuel. Considérons
pour tout $n$ de $\SetN^*$ l'application $f_n$ de $E$ définie par :
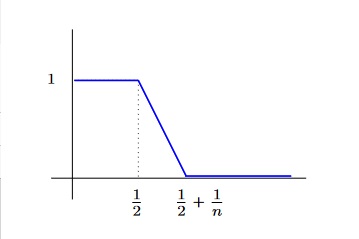
- Montrer que pour tous $p$ et $q$ dans $\SetN$ avec $p>q$, on a : $\|f_p-f_q\|\leq\frac{1}{q}$.
- En déduire que $(f_n)$ est une suite de Cauchy.
- Montrer que si $(f_n)$ converge vers $f$ alors $f$ vaut $1$ sur $[0;\frac{1}{2}]$ et $f$ vaut 0 sur tout intervalle de la forme $[a,1]$ avec $a>\frac{1}{2}$
- En déduire que $(f_n)$ ne converge pas dans $E$.
|
V. Limite et continuité.
V.3. Ouverts/Fermés.
Définition temporaire.
Soit $E$ un espace préhilbertien réel.
- Un sous ensemble $F$ de $E$ est fermé si et seulement si toute suite convergente de $F$ converge dans $F$ c'est-à-dire si et seulement si :
$$\forall l\in E,\:\:\:\forall (u_n)\in F^\SetN\!,\:\:\:\:u_n\tendvers{n}{+\infty}l\:\:\:\Longrightarrow\:\:\:l\in F$$
- Un sous ensemble $O$ de $E$ est ouvert si et seulement si son complémentaire est un fermé.
Exemples.50
Soient $a$, $b$, $c$ et $d$ dans $\SetR$ tels que $a < b$ et $c < d$.
- $]a,b[$, $]a,+\infty[$ et $]-\infty,b[$ sont des ouverts de $\SetR$.
- $[a,b]$, $[a,+\infty[$ et $]-\infty,b]$ sont des fermés de $\SetR$.
- $[a,b]\times [c,d]$ est un fermé de $\SetR^2$
- $[a,b]^n$ est un fermé de $\SetR^n$.
Exercice.51
Notons
$$
A=\left\{\:\left[\begin{array} {ccc}%
a&b\\
c&d\\
\end{array}%
\right]\:\:\:/\:\:\:a,b,c,d\in[0,1]\right\}
\hskip1.5cm
B=\left\{\:\left[\begin{array} {ccc}%
a&b\\
c&d\\
\end{array}%
\right]\:\:\:/\:\:\:a,b,c,d\in\SetR^*\:\right\}
$$
Montrer que $A$ est un fermé et $B$ est un ouvert de $\mathcal{M}_{n}(\SetR)$
|
V. Limite et continuité.
V.4. Limite et continuité d'une application
Définition.
Soient $E$ et $F$ des espaces préhilbertiens réels et $\|.\!.\!.\|_{_E}$, $\|.\!.\!.\|_{_F}$ les normes euclidiennes associées.
Notons $f$ une application d'un sous-ensemble $D$ de $E$ dans $F$.
- Soit $x_0$ dans $E$. L'application $f$ admet une limite $l$ en $x_0$, et on note $\limite{x}{x_0}f(x)=l$, si et seulement si :
$$\forall\varepsilon\in\SetR^*_+,\:\:\exists\eta\in\SetR^*_+,\:\:\forall x\in D_f,\:\:\|x-x_0\|_{_E}\leq\eta\Longrightarrow\|f(x)-l\|_{_F}\leq\varepsilon$$
- Soit $x_0$ dans $D$. L'application $f$ est continue en $x_0$ si et seulement si $\limite{x}{x_0}f(x)=f(x_0)$.
- L'ensemble des applications de $D$ dans $F$ continue est noté $\mathcal{C}(D,F)$.
Remarques.
-
La définition de la limite n'est rien d'autre que la définition de la limite d'une fonction réelle en remplaçant les valeurs absolues par des normes.
-
Si on arrive à montrer que pour tout $x$ de $E$, on a : $${\|f(x)-l\;\|}_{_F}\:\:\leq\:\: \alpha{\|x-x_0\|}^\beta_{_E}$$
avec $\alpha$ et $\beta$ réels positifs, l'application $f$ admet $l$ pour limite en $x_0$ $($on prend $\eta=\left(\frac{\varepsilon}{\alpha}\right)^{\frac{1}{\beta}})$. En pratique, comme par exemple dans l'exercice suivant, on essaie de retrouver cette inégalité.
Exercice.52
Montrer que l'application $f$ de $(\SetR^2,\|.\!.\!.\|_2)$ dans $(\SetR,|.\!.\!.|)$ suivante admet une limite en 0 :
$$f(x,y)=\frac{x^2y^2}{x^2+y^2}$$
|



