Psi - Math - Lycée Alphone Daudet

Liste chapitres

Plan du chapitre

Section

sous-section

V. Limite et continuité.

V.1. Limite d'une suite

Définition.

Soit $E$ un espace vectoriel préhilbertien réel et $\|.\!.\!.\|$ la norme euclidienne associée. La suite $(u_n)$ tend vers un vecteur $l$ de $E$, et on note $\:u_n\tendvers{n}{+\infty}l\:$, si et seulement si : $$\forall\varepsilon\in\SetR^*_+,\:\exists N\in\SetN,\forall n\geq N,\:\|u_n-l\|\leq\varepsilon$$ C'est la définition de la limite d'une suite réelle en remplaçant la valeur absolue par la norme euclidienne.

Caractérisation.^⁴⁶

On peut toujours se ramener à la convergence d'une suite réelle puisque : $$u_n\tendversNorme{\|\:\:\|}l\:\:\:\:\:\:\:\:\Longleftrightarrow\:\:\:\:\:\:\:\:\|u_n-l\|\tendvers{n}{+\infty}0$$

Théorème.^⁴⁷

Une suite $(M_n)$ de $\mathcal{M}_{pq}(\SetR)$ tend vers $M$ si et seulement si les coefficients de $(M_n)$ tendent vers les coefficients de $M$.
Une suite $(x_n)$ de $\SetR^n$ tend vers $x$ si et seulement si les coordonnées de $x_n$ tendent vers les coordonnées de $x$.
Soient $(M_n)$ et $(N_n)$ des suites respectives de $\mathcal{M}_{pq}(\SetR)$ et $\mathcal{M}_{qr}(\SetR)$, alors : $$\left\{\begin{array}{ll} M_n\tendvers{n}{+\infty}{M}\\ N_n\tendvers{n}{+\infty}{N}\\ \end{array}\right. \hskip1cm\Longrightarrow\hskip1cm M_nN_n\tendvers{n}{+\infty}{MN}\\ $$

Exemples.

$$n\left(\begin{array} {ccc}% \arctan\left(\frac{1}{n}\right)\\ \cos\left(\frac{1}{n}\right)-1\\ \end{array}% \right)\:\:\tendvers{n}{+\infty}\:\:\left(\begin{array} {ccc}% 1\\ 0 \end{array}% \right) \hskip2cm \frac{1}{n}\left(\begin{array} {ccc}% (-1)^n&n+1\\ \Haut{0.48}n^2\sin\left(\frac{1}{n}\right)&1 \end{array}% \right)\:\:\tendvers{n}{+\infty}\:\:\left(\begin{array} {ccc}% 0&1\\ \Haut{0.48}1&0 \end{array}% \right)$$

Exercice.^⁴⁸

Soit $\|.\!.\|_2$ la norme euclidienne de $\mathcal{M}_p(\SetR)$. Montrer que : $$\forall A,B\in\mathcal{M}_p(\SetR),\:\:{\|AB\|}_2\:\leq\:{\|A\|}_2{\|B\|}_2$$
Notons $(a_{ii}^k)$ les coefficients de la matrice $A^k$. Montrer que : $$\forall i,j\in\{1,..., p\},\forall k\in\SetN,\:|a_{ij}^k[\:\leq\:{\|A\|}_2^k$$
On définit l'exponentielle complexe par : $$\forall A\in\mathcal{M}_p(\SetR),\:\:e^A\:\=\:\sum_{n=0}^\infty\frac{A^n}{n!}$$ Montrer que cette série converge.
Comment calculer l'exponentielle d'une matrice diagonalisable $A$ de $\mathcal{M}_n(\SetR)$ ?

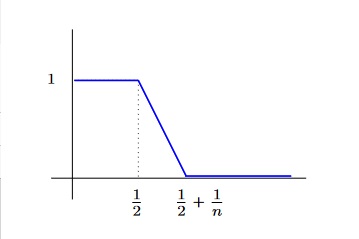
V. Limite et continuité.

V.3. Ouverts/Fermés.

Définition temporaire.

Soit $E$ un espace préhilbertien réel.

Un sous ensemble $F$ de $E$ est fermé si et seulement si toute suite convergente de $F$ converge dans $F$ c'est-à-dire si et seulement si : $$\forall l\in E,\:\:\:\forall (u_n)\in F^\SetN\!,\:\:\:\:u_n\tendvers{n}{+\infty}l\:\:\:\Longrightarrow\:\:\:l\in F$$
Un sous ensemble $O$ de $E$ est ouvert si et seulement si son complémentaire est un fermé.

Exemples.^⁵⁰

Soient $a$, $b$, $c$ et $d$ dans $\SetR$ tels que $a < b$ et $c < d$.

$]a,b[$, $]a,+\infty[$ et $]-\infty,b[$ sont des ouverts de $\SetR$.
$[a,b]$, $[a,+\infty[$ et $]-\infty,b]$ sont des fermés de $\SetR$.
$[a,b]\times [c,d]$ est un fermé de $\SetR^2$
$[a,b]^n$ est un fermé de $\SetR^n$.

Exercice.^⁵¹

Notons $$ A=\left\{\:\left[\begin{array} {ccc}% a&b\\ c&d\\ \end{array}% \right]\:\:\:/\:\:\:a,b,c,d\in[0,1]\right\} \hskip1.5cm B=\left\{\:\left[\begin{array} {ccc}% a&b\\ c&d\\ \end{array}% \right]\:\:\:/\:\:\:a,b,c,d\in\SetR^*\:\right\} $$ Montrer que $A$ est un fermé et $B$ est un ouvert de $\mathcal{M}_{n}(\SetR)$