III. Utilisation et fabrication de familles orthogonales.
III.1. Composantes d'un vecteur dans une BON
Théorème.24
Soient $\left(E,\langle\:,\:\rangle\:\right)$ est un eve et $\beta=(e_1,...,e_n)$ une base orthonormale de $E$. Les coordonnées d'un vecteur $x$ de $E$ peuvent être exprimées à l'aide du pse :
$$x\=\sum_{k=1}^n\langle x,e_k\rangle e_k\hskip2cm x\left(\begin{array} {c}%
\langle x,e_1\rangle \\
\langle x,e_2\rangle \\
\vdots\\
\langle x,e_n\rangle \\
\end{array}%
\right)$$
|
III. Utilisation et fabrication de familles orthogonales.
III.2. Expression du produit scalaire scalaire dans une BON
Théorème.25
Soient $E$ un eve et $\beta=(e_1,...,e_n)$ une base orthonormale de $E$. De plus notons $[x]_{_\beta}=(x_1,...,x_n)$ et $[y]_{_\beta}=(y_1,...,y_n)$ les coordonnées de $x$ et $y$ dans $\beta$, alors :
$$\langle x,y\rangle \=\left\langle [x]_{_\beta},[y]_{_\beta}\right\rangle \=\sum_{i=1}^nx_i.y_i\hskip1cm\hbox{ et }
\hskip1cm \left\|x\right\|^2\=\|[x]_{_\beta}\|^2\=\sum_{i=1}^nx_i^2$$
Dans la deuxième égalité, $\langle.\!.,.\!.\rangle$ et $\|.\!.\|$ représente le produit scalaire usuel sur $\SetR^n$ et la norme euclidienne associée.
Remarques.
- Ainsi dans une BON, le produit scalaire de deux vecteurs est égal au produit scalaire de leurs coordonnées.
- Si la base n'est pas orthonormale, l'expression du produit scalaire peut être beaucoup plus lourde.
|
III. Utilisation et fabrication de familles orthogonales.
III.3. Expression du projeté orthonormal dans une BON
Définition.
Soit $F$ un sev d'un $\SetR$-ev tel que $\ds E=F\mathop{\oplus}^\perp F^\perp$.
La projection orthogonale sur $F$ est la projection sur $F$ de direction $F^\perp$.
Théorème.26
Soient $E$ un pré-hilbertien réel, $F$ un sev de $E$ de dimension finie et
$(e_1,... e_n)$ une BON de $F$. Alors la projection orthogonale sur $F$ existe et :
$$p(x)\=\sum_{k=1}^n\left\langle x,e_k\right\rangle e_k$$
Remarque.
- Ainsi pour que la projection orthogonale sur $F$ existe, il faut et il suffit que $\ds E=F\mathop{\oplus}^\perp F^\perp$.
- Si on considère $Id_{_E}$ comme une projection orthogonale sur $E$, on retrouve à l'aide de ce théorème l'expression des coordonnées d'un vecteur dans une BON.
Exercice - Bessel.27
Soient $(e_n)_{_{n\in\SetN}}$ une famille orthonormale d'un espace pré-hilbertien réel.
- Notons $p_n$ la projection orthogonale sur $F_n=\text{vect}(e_1,...,e_n)$. Exprimer $\|p_n(x)\|^2$ à l'aide de $x$, des $e_i$ et du produit scalaire.
- En déduire que la série $\sum\langle x,e_n\rangle ^2$ est convergente pour tout $x$ de $E$ et $$\sum_{n=0}^{+\infty}\langle x,e_n\rangle ^2\:\:\leq\:\:\|x\|^2$$
C'est l'inégalité de Bessel.
|
III. Utilisation et fabrication de familles orthogonales.
III.4. Procédé d'orthonormalisation de Gram-Schmidt
Théorème.28
Soit $E$ un préhilbertien réel. On va décrire un procédé qui permet de construire une famille orthogonale $(o_1,o_2,...,o_n)$
à partir d'une famille libre $(l_1,l_2,...,l_n)$ de $E$. Construisons le vecteur $o_k$ par récurrence forte :
-
Si $k=1$ on pose $o_1=l_1$
- Supposons que $o_1,...,o_k$ construits, construisons $o_{k+1}$.
$$o_{k+1}\:\=\:l_{k+1}-p(l_{k+1})\:\=\:l_{k+1}\:-\:\sum_{i=1}^k\hbox{$\left\langle l_{k+1},\frac{o_i}{\|o_i\|}\right\rangle \frac{o_i}{\|o_i\|}$}$$
avec $p$ la projection orthogonale de $E$ sur $F_k=Vect(o_1,...,o_k)$.
Vision géométrique de ce qu'on fait.
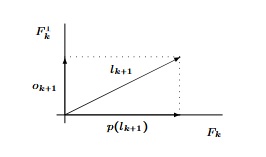
Remarques.
- La famille $\beta=\left(\frac{o_1}{\|o_1\|},...,\frac{o_k}{\|o_k\|}\right)$ est une BON de $F_k$ et l'expression $\ds\sum_{i=1}^k$ $\left\langle l_{k+1},\frac{o_i}{\|o_i\|}\right\rangle \frac{o_i}{\|o_i\|}$
est l'expression du projeté orthogonale de $l_{k+1}$ dans la BON $\beta$.
- Si les premiers vecteurs de la famille sont déjà orthogonaux, l'algorithme ne modifie pas ces vecteurs puisque dans l'expression de $o_{k+1}$ les produits scalaires sont nuls.
- Une fois l'algorithme effectué, on peut très bien rendre la famille $(o_1,..., o_n)$ orthonormale en divisant chaque vecteur par sa norme. On peut aussi donner une autre condition de normalisation. Par exemple s'il s'agit de polynômes, on peut préférer avoir des polynômes unitaires $($coefficient dominant valant 1$)$ plutôt que normés.
Propriétés.
Soit $(o_1,...,o_n)$ la famille orthogonale construite à partir de $(l_1,...,l_n)$ à l'aide du procédé de Gram-Scmidt.
- $\forall
k\in\{1,...,n\},\:\text{Vect}(o_1,...,o_k)=\text{Vect}(l_1,...,l_k)$
- $\forall
k\in\{1,...,n\},\:\left\langle o_k,l_k\right\rangle \:>0$
Exercice.29
Soit $$\left\{\begin{array}{c}
u_1=(1,1,1) \\
u_2=(1,0,1) \\
u_3=(1,1,0) \
\end{array}\right.$$ Effectuer le procédé d'orthonormalisation de
Gram-Scmidt, afin de transformer cette famille libre en base orthonormale.
Exercice.30
On munit $\SetR_2[X]$ muni du produit
scalaire : $$(P/Q)\=\int_{-1}^1P(x)Q(x)dx$$ Utiliser l'algorithme de
Gram-Schmidt pour construire une base othogonale de polynômes unitaires à partir de la famille $\:\left(1,X,X^2\right)\:$.
|



