Psi - Math - Lycée Alphone Daudet

Liste chapitres

Plan du chapitre

Section

sous-section

III. Utilisation et fabrication de familles orthogonales.

III.2. Expression du produit scalaire scalaire dans une BON

Théorème.^²⁵

Soient $E$ un eve et $\beta=(e_1,...,e_n)$ une base orthonormale de $E$. De plus notons $[x]_{_\beta}=(x_1,...,x_n)$ et $[y]_{_\beta}=(y_1,...,y_n)$ les coordonnées de $x$ et $y$ dans $\beta$, alors : $$\langle x,y\rangle \=\left\langle [x]_{_\beta},[y]_{_\beta}\right\rangle \=\sum_{i=1}^nx_i.y_i\hskip1cm\hbox{ et } \hskip1cm \left\|x\right\|^2\=\|[x]_{_\beta}\|^2\=\sum_{i=1}^nx_i^2$$ Dans la deuxième égalité, $\langle.\!.,.\!.\rangle$ et $\|.\!.\|$ représente le produit scalaire usuel sur $\SetR^n$ et la norme euclidienne associée.

Remarques.

Ainsi dans une BON, le produit scalaire de deux vecteurs est égal au produit scalaire de leurs coordonnées.
Si la base n'est pas orthonormale, l'expression du produit scalaire peut être beaucoup plus lourde.

III. Utilisation et fabrication de familles orthogonales.

III.4. Procédé d'orthonormalisation de Gram-Schmidt

Théorème.^²⁸

Soit $E$ un préhilbertien réel. On va décrire un procédé qui permet de construire une famille orthogonale $(o_1,o_2,...,o_n)$ à partir d'une famille libre $(l_1,l_2,...,l_n)$ de $E$. Construisons le vecteur $o_k$ par récurrence forte :

Si $k=1$ on pose $o_1=l_1$
Supposons que $o_1,...,o_k$ construits, construisons $o_{k+1}$. $$o_{k+1}\:\=\:l_{k+1}-p(l_{k+1})\:\=\:l_{k+1}\:-\:\sum_{i=1}^k\hbox{$\left\langle l_{k+1},\frac{o_i}{\|o_i\|}\right\rangle \frac{o_i}{\|o_i\|}$}$$ avec $p$ la projection orthogonale de $E$ sur $F_k=Vect(o_1,...,o_k)$.

Vision géométrique de ce qu'on fait.

Remarques.

La famille $\beta=\left(\frac{o_1}{\|o_1\|},...,\frac{o_k}{\|o_k\|}\right)$ est une BON de $F_k$ et l'expression $\ds\sum_{i=1}^k$ $\left\langle l_{k+1},\frac{o_i}{\|o_i\|}\right\rangle \frac{o_i}{\|o_i\|}$ est l'expression du projeté orthogonale de $l_{k+1}$ dans la BON $\beta$.
Si les premiers vecteurs de la famille sont déjà orthogonaux, l'algorithme ne modifie pas ces vecteurs puisque dans l'expression de $o_{k+1}$ les produits scalaires sont nuls.
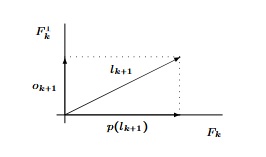
Une fois l'algorithme effectué, on peut très bien rendre la famille $(o_1,..., o_n)$ orthonormale en divisant chaque vecteur par sa norme. On peut aussi donner une autre condition de normalisation. Par exemple s'il s'agit de polynômes, on peut préférer avoir des polynômes unitaires $($coefficient dominant valant 1$)$ plutôt que normés.

Propriétés.

Soit $(o_1,...,o_n)$ la famille orthogonale construite à partir de $(l_1,...,l_n)$ à l'aide du procédé de Gram-Scmidt.

$\forall k\in\{1,...,n\},\:\text{Vect}(o_1,...,o_k)=\text{Vect}(l_1,...,l_k)$
$\forall k\in\{1,...,n\},\:\left\langle o_k,l_k\right\rangle \:>0$

Exercice.^²⁹

Soit $$\left\{\begin{array}{c} u_1=(1,1,1) \\ u_2=(1,0,1) \\ u_3=(1,1,0) \ \end{array}\right.$$ Effectuer le procédé d'orthonormalisation de Gram-Scmidt, afin de transformer cette famille libre en base orthonormale.

Exercice.^³⁰

On munit $\SetR_2[X]$ muni du produit scalaire : $$(P/Q)\=\int_{-1}^1P(x)Q(x)dx$$ Utiliser l'algorithme de Gram-Schmidt pour construire une base othogonale de polynômes unitaires à partir de la famille $\:\left(1,X,X^2\right)\:$.